La roue
La force entre la route et la roue
Comme entre deux surfaces quelconques, la force de contact entre la route et la roue a deux composantes :
- une composante perpendiculaire à la surface de contact : N
- une composante tangentielle à la surface de contact (force de frottement) : F
Si la roue glisse sur la route, alors F=μkN.
Si la roue roule ,sans glisser, sur la route, alors 0 ≤ F ≤ μsN.
Dans tous les cas la force F s'oppose au mouvement relatif entre les deux surfaces.
La résistance au roulement (rolling resistance)
L'expérience nous dit qu'une roue seule roulant sur une surface horizontale va finir par s'arrêter de rouler. La force F ne peut pas expliquer à elle seule cet effet, puisque son moment contribue à accélérer la rotation de la roue (voir ci-bas)!
En réalité, lors du roulement,
- Le devant de la roue vient appuyer sur le sol. Le sol et la roue se déforment. De l'énergie est donnée aux atomes du sol et de la roue... le roulement entraîne donc une perte d'énergie (l'énergie cinétique devient de l'énergie thermique et est éventuellement dissipée en chaleur).
- Le derrière de la roue se décolle du sol. Ce décollage nécessite également une légère force (le sol « retient » un peu la roue!)
Tout ceci peut être modélisé en plaçant la force N à une distance « b » devant le centre de la roue. Note : la déformation est ici grandement exagérée!!!
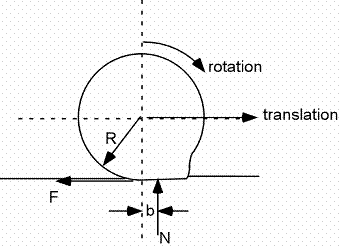
Cette distance b dépend :
- Des matériaux formant la roue et le sol (la résistance est plus grande si on fait du vélo sur le sable mou plutôt que sur l'asphalte!). Un pneu bien gonflé, par exemple, a un plus petit « b ».
- Un peu de la vitesse. Nous négligerons cette dépendance lors de nos analyses.
Note :
Souvent on parle d'un coefficient de friction de roulement : μ R = b/R où R est le rayon de la roue.
Pour un pneu de caoutchouc sur du béton, les ordres de grandeur mentionnés sont généralement :
- μR ≈ 0.01
- μk ≈ 0.8
- μs ≈ 0.9
En général, on ne peut pas dire que F vaut μRN lors d'un roulement (sauf cas bien particuliers).
Il arrive fréquemment que, dans les livres, on néglige la résistance au roulement. Cela est fait pour simplifier les problèmes et ce n'est souvent pas plus dramatique que de négliger la résistance de l'air. Si on veut retrouver les résultats sans résistance au roulement, posez μ R (ou b) = 0. Bien sûr à ce moment une roue roulant sur une surface plane ne s'arrêtera jamais, pas plus qu'une bille placée dans un puits en U...