La roue
| Site: | ÉTS - Environnement numérique d’apprentissage |
| Cours: | ING150 Statique et dynamique |
| Livre: | La roue |
| Imprimé par: | Visiteur anonyme |
| Date: | dimanche, 1 février 2026, 17:49 |
Table des matières
- La roue - A. Hénault
- La force entre la route et la roue
- La roue et la statique
- Cinématique de la roue
- Exemple 1A - Roue qui décélère sur un plan horizontal
- Énergie 1A - Roue qui décélère sur un plan horizontal
- Exemple 1B - Roue qui bouge à vitesse constante
- Énergie 1B - Roue qui bouge à vitesse constante sur un plan horizontal
- Exemple 1C - Roue qui accélère sur un plan horizontal
- Énergie 1C - Roue qui accélère sur un plan horizontal
- Exemple 1D - Roue sur une pente descendante
- Énergie 1D - Roue sur une pente descendante
- Exemple 1E - Roue sur une pente ascendante
- Énergie 1E - Roue sur une pente ascendante
- Exemple 1F - Roue accélérée grâce à un couple
- Énergie 1F - Roue accélérée grâce à un couple
- Exemple 1G - Roue décélérée grâce à un couple (freins)
- Énergie 1G - Roue décélérée grâce à un couple de freinage
- Exemple 2A - Bicyclette accélérée
- Énergie 2A - Bicyclette accélérée
- Exemple 2B - Bicyclette en freinage (roue avant)
- Énergie 2B - Bicyclette en freinage (roue avant)
- Exemple 3A - Automobile accélérée
- Énergie 3A - Automobile accélérée
- Exemple 3B - Automobile en freinage
- Énergie 3B - Automobile et freinage
- La 2ème loi de Newton - les forces
- La 2ème loi de Newton - les moments
- Centre de masse
- Travail fait par un couple lors d'une rotation
- Énergie cinétique de rotation
La roue - A. Hénault
La roue, voilà une structure typique de la mécanique... Tellement typique même, qu'en prononçant le mot "mécanique", il est difficile de ne pas penser à un objet monté sur roues... N'est-ce pas ?

Dans le cours de Statique et Dynamique (ING-150), par manque de temps, on ne peut faire virtuellement aucune dynamique de rotation, qui est essentielle pour la compréhension de cette structure ultra-typique qu'est la roue.... C'est bien triste. Certains de nos ingénieurs (même ceux qui ne sont pas en génie mécanique) peuvent participer à des projets où on modélise des chariots, des robots sur roue, des automobiles, qui sait ?
Alors voici quelques principes de base et exemples qui pourront satisfaire , si vous en sentez le besoin, votre curiosité. Dans tous les exemples, on utilise l'approche forces et moments et l'approche énergie. Si vous désirez savoir d'où vient une relation, il y a souvent un lien vers une démonstration, par exemple, si vous cliquez sur la relation fondamentale ci-dessous, il y a un lien vers sa démonstration.
Note : ce complément va un peu (mais pas beaucoup) plus loin que le cours ING-150. Je pense que toutes les notions sont à votre portée!
La table des matières se trouve ci-contre, à droite.
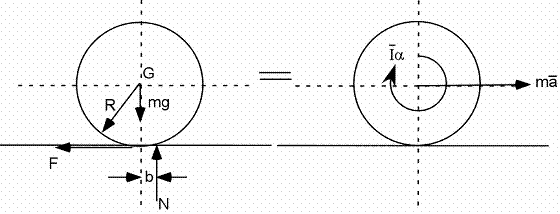
La force entre la route et la roue
Comme entre deux surfaces quelconques, la force de contact entre la route et la roue a deux composantes :
- une composante perpendiculaire à la surface de contact : N
- une composante tangentielle à la surface de contact (force de frottement) : F
Si la roue glisse sur la route, alors F=μkN.
Si la roue roule ,sans glisser, sur la route, alors 0 ≤ F ≤ μsN.
Dans tous les cas la force F s'oppose au mouvement relatif entre les deux surfaces.
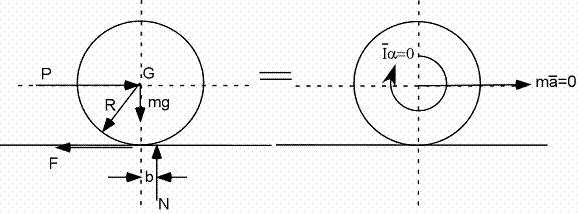
La résistance au roulement (rolling resistance)
L'expérience nous dit qu'une roue seule roulant sur une surface horizontale va finir par s'arrêter de rouler. La force F ne peut pas expliquer à elle seule cet effet, puisque son moment contribue à accélérer la rotation de la roue (voir ci-bas)!
En réalité, lors du roulement,
- Le devant de la roue vient appuyer sur le sol. Le sol et la roue se déforment. De l'énergie est donnée aux atomes du sol et de la roue... le roulement entraîne donc une perte d'énergie (l'énergie cinétique devient de l'énergie thermique et est éventuellement dissipée en chaleur).
- Le derrière de la roue se décolle du sol. Ce décollage nécessite également une légère force (le sol « retient » un peu la roue!)
Tout ceci peut être modélisé en plaçant la force N à une distance « b » devant le centre de la roue. Note : la déformation est ici grandement exagérée!!!
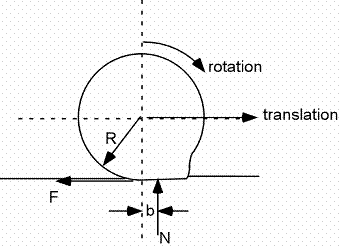
Cette distance b dépend :
- Des matériaux formant la roue et le sol (la résistance est plus grande si on fait du vélo sur le sable mou plutôt que sur l'asphalte!). Un pneu bien gonflé, par exemple, a un plus petit « b ».
- Un peu de la vitesse. Nous négligerons cette dépendance lors de nos analyses.
Note :
Souvent on parle d'un coefficient de friction de roulement : μ R = b/R où R est le rayon de la roue.
Pour un pneu de caoutchouc sur du béton, les ordres de grandeur mentionnés sont généralement :
- μR ≈ 0.01
- μk ≈ 0.8
- μs ≈ 0.9
En général, on ne peut pas dire que F vaut μRN lors d'un roulement (sauf cas bien particuliers).
Il arrive fréquemment que, dans les livres, on néglige la résistance au roulement. Cela est fait pour simplifier les problèmes et ce n'est souvent pas plus dramatique que de négliger la résistance de l'air. Si on veut retrouver les résultats sans résistance au roulement, posez μ R (ou b) = 0. Bien sûr à ce moment une roue roulant sur une surface plane ne s'arrêtera jamais, pas plus qu'une bille placée dans un puits en U...
La roue et la statique
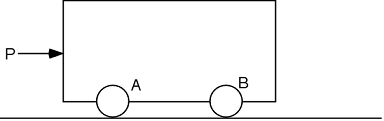
Dans ce problème de statique, la roue A peut tourner librement et la roue B est bloquée par un frein. On demande les réactions en A et B (par exemple).
- Quand on fait le diagramme de forces (DCL) de cet objet, il n'y a pas de force de frottement en A. Pourquoi ?
S'il y avait une force de frottement (exercée par le sol) sur la roue A, le DCL de la roue A serait
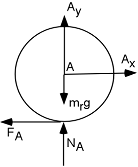
et alors la somme des moments par rapport au point A ne serait pas nulle et la roue A ne pourrait pas être statique!
Note : il n'y a pas de résistance au roulement quand la roue ne roule pas! NA n'est pas déplacée par rapport au centre de la roue.
- Et pour la roue B?
Comme la roue B est bloquée par un frein, son DCL est :
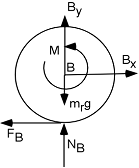
M est le couple de freinage et s'oppose au moment de F B . La roue B peut donc tenir en équilibre même en présence de F B .
Le DCL de l'objet est donc :
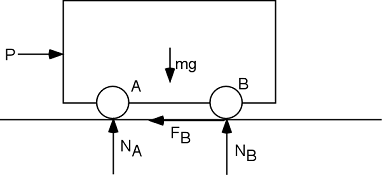
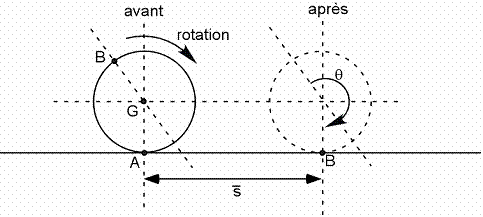
Cinématique de la roue
La roue de rayon R roule et passe de la situation 1 (avant) à la situation 2 (après). La roue a tourné d'un angle θ . Si on détachait la ligne qui va de A à B et qu'on la déroulait par terre, cette ligne serait de longueur Rθ . On voit que ![]() est la longueur de cette ligne.
est la longueur de cette ligne.
Bref:
- La distance parcourue par le centre de masse :
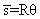
- La vitesse du centre de masse est
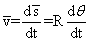 ou encore
ou encore 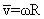 ( ω: vitesse angulaire (rad/s))
( ω: vitesse angulaire (rad/s))
- L'accélération du centre de masse est
 ou encore
ou encore 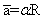 ( α: accélération angulaire (rad/s))
( α: accélération angulaire (rad/s))
Énergie 1A - Roue qui décélère sur un plan horizontal
Comment transformer « forces et moments » en énergie :
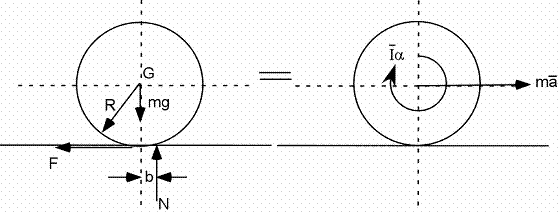
Forces et moments :
|
|
1. On multiplie l'équation « forces » par ![]() et l'équation « moments » par dθ
et l'équation « moments » par dθ
![]()
2. On se sert des 2 relations :
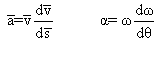
Alors on obtient :
![]()
3. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
4. On intègre, en considérant que la roue a roulé sur une distance d (= ![]() ) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Énergie perdue par roulement = Baisse de l'énergie cinétique de rotation+ Baisse de l'énergie cinétique de translation.
Énergie 1B - Roue qui bouge à vitesse constante sur un plan horizontal
Comment transformer « forces et moments » en énergie :
Forces et moments :
|
|
1. On multiplie l'équation forces par ![]() et l'équation moments par dθ
et l'équation moments par dθ
![]()
2. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
3. On intègre, en considérant que la roue a roulé sur une distance d (=![]() ) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Travail de la force P– énergie perdue par roulement = 0
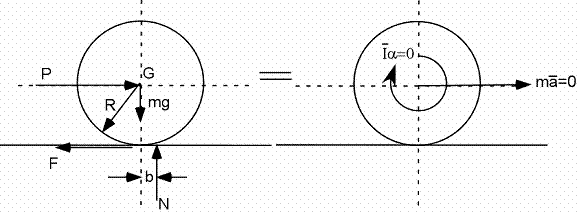
Exemple 1C - Roue qui accélère sur un plan horizontal
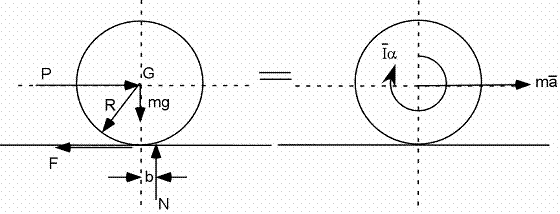
Forces et moments :
Et comme ![]() et
et ![]()
alors ![]() et
et ![]()
Note : F ne doit pas dépasser μs N pour qu'il y ait roulement.
Énergie :
Travail de la force P – énergie perdue par roulement = Augmentation de l'énergie cinétique de rotation+ Augmentation de l'énergie cinétique de translation.
Énergie 1C - Roue qui accélère sur un plan horizontal
Comment transformer forces et moments en énergie :
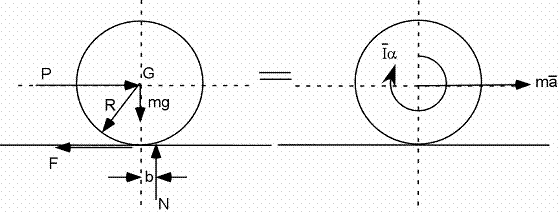
Forces et moments :
|
|
1. On multiplie l'équation forces par ![]() et l'équation moments par dθ
et l'équation moments par dθ
![]()
2. On se sert des 2 relations :
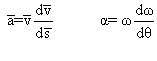
Alors on obtient :
![]()
3. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
4. On intègre, en considérant que la roue a roulé sur une distance d (= ![]() ) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Travail de la force P – énergie perdue par roulement = Augmentation de l'énergie cinétique de rotation+ Augmentation de l'énergie cinétique de translation.
Exemple 1D - Roue sur une pente descendante
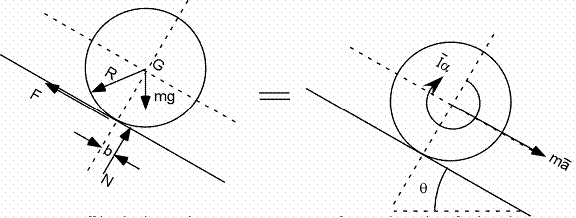
Forces et moments :
Et comme ![]() et
et ![]()
alors ![]() et
et ![]()
Note : F ne doit pas dépasser μs N pour qu'il y ait roulement.
Énergie :
Travail de la gravité – énergie perdue par roulement = Augmentation de l'énergie cinétique de rotation+ Augmentation de l'énergie cinétique de translation.
Énergie 1D - Roue sur une pente descendante
Comment transformer « forces et moments » en énergie :
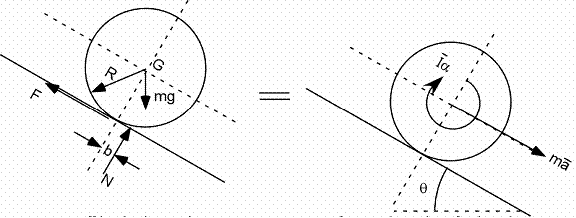
Forces et moments :
|
|
1. On multiplie l'équation forces par ![]() et l'équation moments par dθ
et l'équation moments par dθ
![]()
2. On se sert des 2 relations :
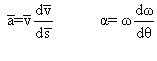
Alors on obtient :
![]()
3. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
4. On intègre, en considérant que la roue a roulé sur une distance d (= ![]() ) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Travail de la gravité – énergie perdue par roulement = Augmentation de l'énergie cinétique de rotation+ Augmentation de l'énergie cinétique de translation.
Exemple 1E - Roue sur une pente ascendante

Forces et moments :
Et comme ![]() et
et ![]()
alors ![]() et
et ![]()
Note : F peut ici être négative, ici : dans ce cas, elle est dirigée dans l'autre sens. La grandeur de F ne doit pas dépasser μs N pour qu'il y ait roulement.
Énergie :
Travail (négatif) de la gravité - énergie perdue par roulement = Variation (négative) de l'énergie cinétique de rotation et de l'énergie cinétique de translation.
Énergie 1E - Roue sur une pente ascendante
Comment transformer « forces et moments » en énergie :
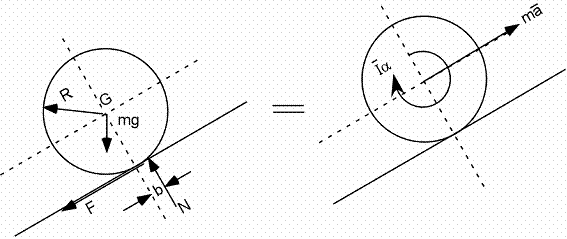
Forces et moments :
|
|
1. On multiplie l'équation forces par ![]() et l'équation moments par dθ
et l'équation moments par dθ
![]()
2. On se sert des 2 relations :
Alors on obtient :
![]()
3. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
4. On intègre, en considérant que la roue a roulé sur une distance d (= ![]() ) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Travail (négatif) de la gravité - énergie perdue par roulement = Variation (négative) de l'énergie cinétique de rotation et de l'énergie cinétique de translation.
Exemple 1F - Roue accélérée grâce à un couple
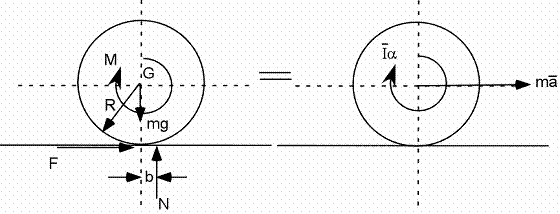
Forces et moments :
Et comme ![]() et
et ![]()
alors ![]() et
et ![]()
Note : La grandeur de F ne doit pas dépasser μs N pour qu'il y ait roulement. Par exemple, sur la glace, si M est trop grand, la roue va tourner à vide sur la route.
Énergie :
Travail du couple - énergie perdue par roulement = Augmentation de l'énergie cinétique de rotation+ Augmentation de l'énergie cinétique de translation.
Énergie 1F - Roue accélérée grâce à un couple
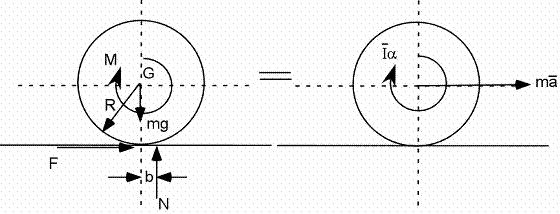
Forces et moments :
|
|
1. On multiplie l'équation forces par ![]() et l'équation moments par d θ
et l'équation moments par d θ
![]()
2. On se sert des 2 relations :
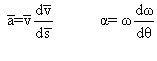
Alors on obtient :
![]()
3. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
4. On intègre, en considérant que la roue a roulé sur une distance d (= ![]() ) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Travail du couple- énergie perdue par roulement = Augmentation de l'énergie cinétique de rotation+ Augmentation de l'énergie cinétique de translation.
Exemple 1G - Roue décélérée grâce à un couple (freins)
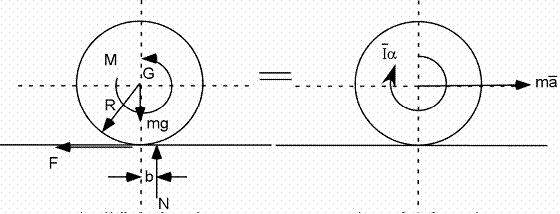
Forces et moments :
Et comme ![]() et
et ![]()
alors ![]() et
et ![]()
Notes :
- La grandeur de F ne doit pas dépasser μs N pour qu'il y ait roulement. Si M est trop grand, la roue va glisser.
- Les freins ABS sont conçus pour que M ne dépasse pas sa valeur maximale (dans cette situation F = μs N ).
Énergie :
Travail (négatif) du couple - énergie perdue par roulement = Variation (négative) de l'énergie cinétique de rotation et de l'énergie cinétique de translation.
Note :
L'énergie perdue (par roulement et surtout via le couple de freinage) est distribuée aux atomes de la roue, des freins et de l'air, sous forme d'énergie thermique. Ceci se traduit par une augmentation de la température de la roue, des freins et de l'air. L'énergie thermique va être ensuite distribuée (sous forme de chaleur ) là où la température est plus faible .
Dans les autos électriques, ou hybrides, l'énergie perdue via le couple de freinage est reconvertie en énergie électrique (on parle de regénération ). C'est l'un des grands avantages de ce type de véhicule.
Énergie 1G - Roue décélérée grâce à un couple de freinage
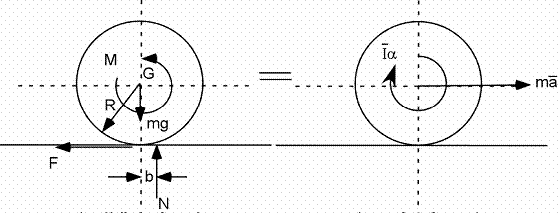
Forces et moments :
|
|
1. On multiplie l'équation forces par ![]() et l'équation moments par dθ
et l'équation moments par dθ
![]()
2. On se sert des 2 relations :
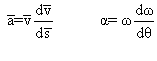
Alors on obtient :
![]()
3. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
4. On intègre, en considérant que la roue a roulé sur une distance d (= ![]() ) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et a tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Travail (négatif) du couple - énergie perdue par roulement = Variation (négative) de l'énergie cinétique de rotation et de l'énergie cinétique de translation.
Exemple 2A - Bicyclette accélérée
Notes :
- le cycliste n'est pas dessiné, mais il est là !
- On a omis la résistance de l'air (qui n'est pas négligeable, généralement), pour simplifier.
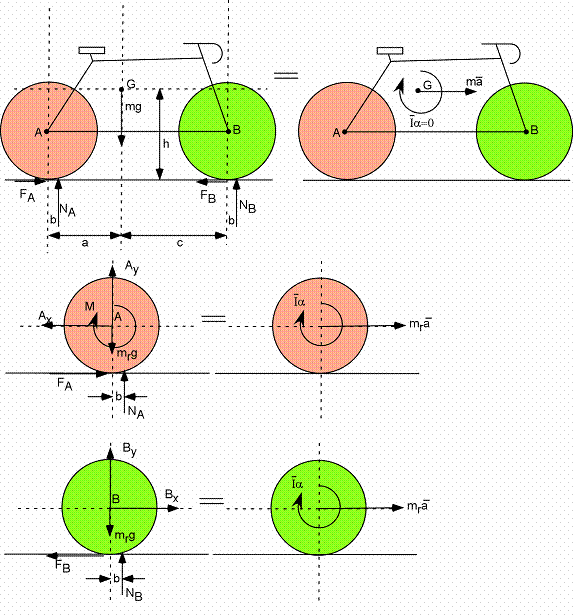
Bicyclette :
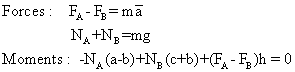
En combinant ces équations on trouve :
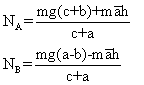
donc (comme c>a) N A> NB... Et NB peut même tomber à 0!
Roue arrière :
![]()
Roue avant :
![]()
En additionnant les équations de moment sur les deux roues et comme ![]() et
et ![]() :
:
![]()
et alors :
![]()
Si M devient trop grand, FA peut dépasser μs NA et la roue peut glisser.
Énergie :
Travail du couple (fourni par le cycliste)- énergie perdue par roulement = Augmentation de l'énergie cinétique de rotation (2 roues)+ Augmentation de l'énergie cinétique de translation.
Note : la résistance de l'air implique une perte d'énergie supplémentaire.
Énergie 2A - Bicyclette accélérée

![]()
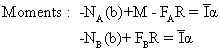
1. On multiplie l'équation forces par ![]() et l'équation moments (on additionne les 2 équations) par dθ
et l'équation moments (on additionne les 2 équations) par dθ
![]()
2. On se sert des 2 relations :
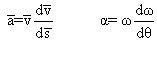
Alors on obtient :
![]()
3. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
4. On intègre, en considérant que les roues (et la bicyclette) ont roulé sur une distance d (= ![]() ) et ont tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et ont tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Travail du couple (fourni par le cycliste)- énergie perdue par roulement = Augmentation de l'énergie cinétique de rotation (2 roues)+ Augmentation de l'énergie cinétique de translation.
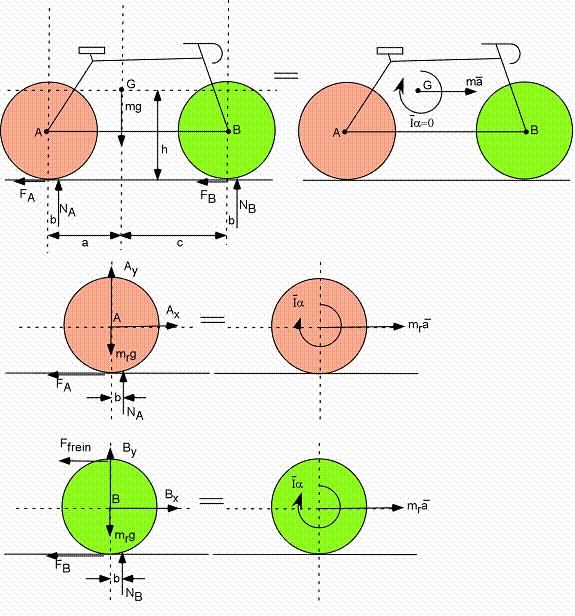
Exemple 2B - Bicyclette en freinage (roue avant)
Notes :
- Le cycliste n'est pas dessiné, mais il est là !
- On a omis la résistance de l'air (qui n'est pas négligeable, généralement), pour simplifier.
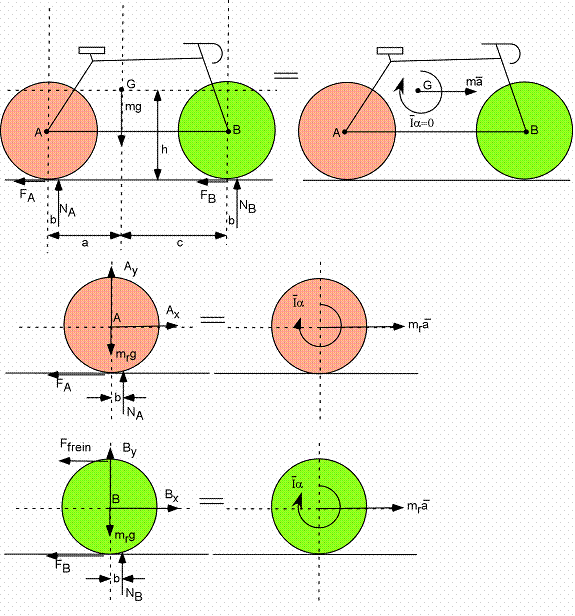
Bicyclette :
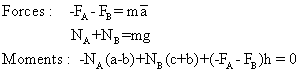
En combinant ces équations on trouve :
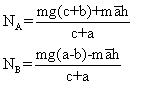
ici NA > NB ou NB > NA ..... tout dépend de ![]() . Si la décélération est trop grande (
. Si la décélération est trop grande ( ![]() très négative), alors NA peut atteindre 0 et la bicyclette peut théoriquement basculer... En réalité, il y a souvent glissement plutôt que basculement.
très négative), alors NA peut atteindre 0 et la bicyclette peut théoriquement basculer... En réalité, il y a souvent glissement plutôt que basculement.
Remarque : si le freinage est sur la roue arrière, il ne peut y avoir basculement (il ne peut y avoir, à l'arrière, à la fois freinage et perte de contact !).
Roue arrière :
![]()
Roue avant :
![]()
En additionnant les équations de moment sur les deux roues et comme ![]() et
et ![]() :
:
![]()
et alors :
![]()
Si Ffrein devient trop grand, FB peut dépasser μs NB et la roue peut glisser.
Énergie :
Travail de freinage (négatif)- énergie perdue par roulement = Variation (négative) de l'énergie cinétique de rotation (2 roues) et de l'énergie cinétique de translation.
Note : la résistance de l'air implique une perte d'énergie supplémentaire.
Énergie 2B - Bicyclette en freinage (roue avant)
![]()
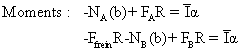
1. On multiplie l'équation forces par ![]() et l'équation moments (on additionne les 2 équations) par dθ
et l'équation moments (on additionne les 2 équations) par dθ
![]()
2. On se sert des 2 relations :
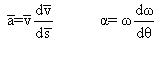
Alors on obtient :
![]()
3. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
4. On intègre, en considérant que les roues (et la bicyclette) ont roulé sur une distance d (= ![]() ) et ont tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et ont tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Travail de freinage (négatif)- énergie perdue par roulement = Variation (négative) de l'énergie cinétique de rotation (2 roues) et de l'énergie cinétique de translation.
Exemple 3A - Automobile accélérée
Notes :
- Il s'agit d'une traction avant, et le moteur est à l'avant.
- On a omis la résistance de l'air, pour simplifier.

Automobile :
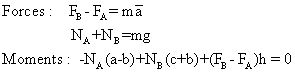
Les deux roues arrière :
![]()
Les deux roues avant :
![]()
En additionnant les équations de moment sur les quatre roues et comme ![]() et
et ![]() :
:
![]()
et alors :
![]()
Si M devient trop grand, FB peut dépasser μs NB et la roue peut glisser, et même tourner à vide (sur la glace, μs est beaucoup plus petit que sur l'asphalte, et ce cas se produit trop souvent!)
Note 1 : 2mr = masse des 2 roues + masse de l'essieu. 2I = moment d'inertie des 2 roues+ celui de l'essieu.
Note 2 : le moment d'inertie de chaque roue vaut ![]() . La masse des roues mr est petite devant la masse totale m de l'auto. Une analyse qui négligerait les moments d'inertie ne serait pas très loin de la réalité.
. La masse des roues mr est petite devant la masse totale m de l'auto. Une analyse qui négligerait les moments d'inertie ne serait pas très loin de la réalité.
Énergie :
Travail du couple (fourni par le moteur) – énergie perdue par roulement = Augmentation de l'énergie cinétique de rotation (4 roues)+ Augmentation de l'énergie cinétique de translation.
Note : la résistance de l'air implique une perte d'énergie supplémentaire.
En fait, si on désire être plus général (l'auto monte/descend une côte) :
L'énergie fournie par le moteur aux roues (via le couple)+travail de la gravité (positif si l'auto descend, négatif si l'auto monte) = augmentation de l'énergie cinétique de translation de l'automobile +augmentation de l'énergie cinétique de rotation des 4 roues +énergie perdue par roulement+énergie perdue par frottement avec l'air .
Si on veut parler de puissance plutôt que d'énergie :
La puissance fournie par le moteur = Mω . Elle peut être exprimée en watts (SI) ou en chevaux-vapeur (système anglais).
La puissance de la gravité est : mgsinθ v.
La puissance perdue par friction dans l'air s'exprime comme : Cv3 où C est un facteur qui dépend de la forme de l'automobile.
![]()
Puissance fournie par le moteur aux roues ± puissance de la gravité (+ si l'auto descend, - si l'auto monte) –puissance perdue par roulement – puissance perdue par friction dans l'air = Puissance requise pour l'accélération (en translation et en rotation).
Énergie 3A - Automobile accélérée
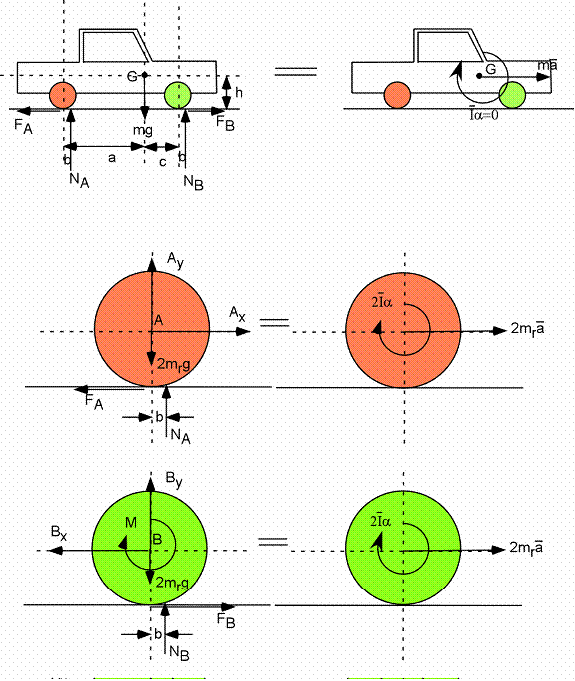
![]()
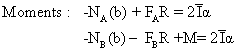
1. On multiplie l'équation forces par ![]() et l'équation moments (on additionne les 2 équations) par dθ
et l'équation moments (on additionne les 2 équations) par dθ
![]()
2. On se sert des 2 relations :
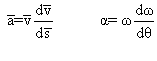
Alors on obtient :
![]()
3. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
4. On intègre, en considérant que les roues (et l'automobile) ont roulé sur une distance d (= ![]() ) et ont tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et ont tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Travail du couple (fourni par le moteur) – énergie perdue par roulement = Augmentation de l'énergie cinétique de rotation (4 roues)+ Augmentation de l'énergie cinétique de translation.
Puissance :
On divise la relation(3) par dt et on obtient :
![]()
Puissance fournie par le moteur – puissance perdue par roulement= Puissance requise pour l'accélération (en translation et en rotation).
Exemple 3B - Automobile en freinage
Note : le freinage se fait aux quatre roues.
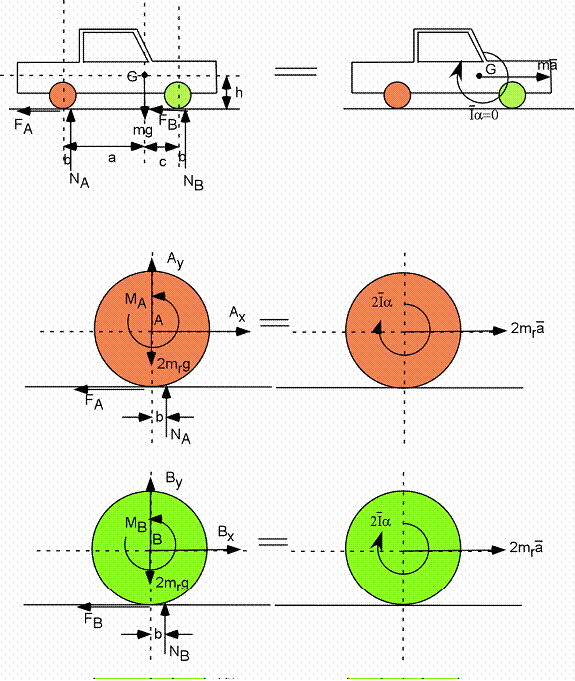
Automobile :

En combinant ces équations on trouve :

Comme b<<a , b<<c , c<a et l'accélération négative, NB >N A
Les deux roues arrière :
![]()
Les deux roues avant :
![]()
En additionnant les équations de moment sur les quatre roues et comme ![]() et
et ![]()
![]()
et alors :
![]()
![]()
Si MB et/ou M A devient trop grand, FB et/ou FA peut/peuvent dépasser μs N et les roues peuvent glisser.
Si le freinage est maximal sur les deux roues (F= μs N), et qu'on isole les couples de freinage :
![]()
![]()
Comme NB >N A , alors MB >M A. Comme le couple de freinage est plus grand à l'avant, l'usure des freins devrait être plus grande à l'avant qu'à l'arrière.
Note 1 : 2mr = masse des 2 roues + masse de l'essieu. 2I = moment d'inertie des 2 roues + celui de l'essieu.
Note 2 : le moment d'inertie de chaque roue vaut ![]() . La masse des roues mr est petite devant la masse totale m de l'auto. Une analyse qui négligerait les moments d'inertie ne serait pas très loin de la réalité.
. La masse des roues mr est petite devant la masse totale m de l'auto. Une analyse qui négligerait les moments d'inertie ne serait pas très loin de la réalité.
Énergie :
Travail des couples de freinage (négatif)– énergie perdue par roulement = Variation négative de l'énergie cinétique de rotation (4 roues) et de l'énergie cinétique de translation.
Note : la résistance de l'air implique une perte d'énergie supplémentaire.
Note :
L'énergie perdue (par roulement et surtout via le couple de freinage) est distribuée aux atomes de la roue, des freins et de l'air, sous forme d'énergie thermique. Ceci se traduit par une augmentation de la température de la roue, des freins et de l'air. L'énergie thermique va être ensuite distribuée (sous forme de chaleur) là où la température est plus faible .
Dans les autos électriques, ou hybrides, l'énergie perdue via le couple de freinage est reconvertie en énergie électrique (on parle de regénération). C'est l'un des grands avantages de ce type de véhicule.
Énergie 3B - Automobile et freinage

![]()
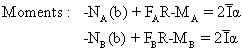
1. On multiplie l'équation forces par ![]() et l'équation moments (on additionne les 2 équations) par dθ
et l'équation moments (on additionne les 2 équations) par dθ
![]()
2. On se sert des 2 relations :
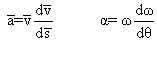
Alors on obtient :
![]()
3. On se sert de ![]() et on substitue une équation dans l'autre, en éliminant F.
et on substitue une équation dans l'autre, en éliminant F.
![]()
4. On intègre, en considérant que les roues (et l'automobile) ont roulé sur une distance d (= ![]() ) et ont tourné d'un angle θ en passant de l'état 1 à l'état 2.
) et ont tourné d'un angle θ en passant de l'état 1 à l'état 2.
![]()
Travail des couples de freinage (négatif)– énergie perdue par roulement = Variation négative de l'énergie cinétique de rotation (4 roues) et de l'énergie cinétique de translation.
La 2ème loi de Newton - les forces
La 2ème loi de Newton pour un objet (système) composé de plusieurs particules.
I) Les forces.
Voici un système composé de trois particules. Les forces sont des forces externes ; les forces sont des forces internes (entre les particules du système).
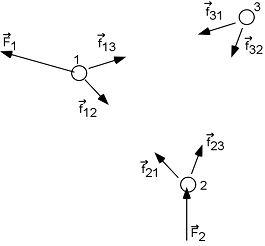
Pour la particule 1 : ![]()
Pour la particule 2 : ![]()
Pour la particule 3 : ![]()
Si on additionne ces 3 équations, et sachant que les forces internes s'annulent deux à deux (exemple : ![]() ), alors on obtient :
), alors on obtient :
![]()
c'est-à-dire : ![]()
La somme des forces externes sur un système = (masse du système)(accélération du centre de masse du système).
La 2ème loi de Newton - les moments
La 2ème loi de Newton pour un objet (système) composé de plusieurs particules.
II) Les moments.
Toujours le même système. Occupons-nous des moments de force par rapport à G.
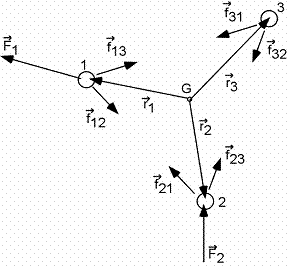
![]()
A) D'une part : ceci devient (en se servant de ![]() )
)
![]()
Mais ![]() car
car ![]() est parallèle à
est parallèle à ![]() (voir figure ci-dessous). Même chose pour les deux termes suivants.
(voir figure ci-dessous). Même chose pour les deux termes suivants.
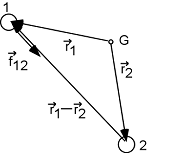
Bref :
![]()
Seules les forces externes comptent dans la somme des moments .
B) D'autre part : ceci devient :
![]()
Plaçons-nous maintenant dans le cas où
- les particules se déplacent dans un plan xy.
- Le système est un objet rigide. Donc la grandeur de
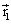 ,
, 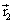 ou
ou 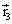 ne peuvent changer.
ne peuvent changer.
On sait déjà (voir chapitre 11) que :
![]() ou
ou ![]()
donc ![]()
Comme la grandeur de ![]() ne change pas, le mouvement relatif de la particule #1 par rapport à G décrit un arc de cercle et
ne change pas, le mouvement relatif de la particule #1 par rapport à G décrit un arc de cercle et ![]() a deux composantes :
a deux composantes : ![]() et
et ![]() (accélération normale et tangentielle).
(accélération normale et tangentielle).
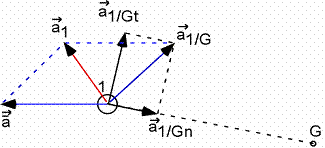
alors ![]()
Maintenant :
- comme
 est parallèle à
est parallèle à 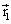 ,
, 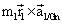 =0
=0
- comme
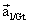 est perpendiculaire à
est perpendiculaire à 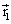 et que
et que 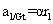 ,
, 
alors : ![]()
et : ![]()
Mais :
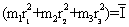 où I est le moment d'inertie de masse par rapport à G (de façon plus générale I est défini comme
où I est le moment d'inertie de masse par rapport à G (de façon plus générale I est défini comme 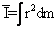 ).
).
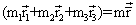 , mais comme l'origine des vecteurs est placée en G,
, mais comme l'origine des vecteurs est placée en G, 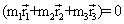
Bref : ![]()
ou, comme tous les moments sont en ±![]() , simplement :
, simplement :
![]()
Centre de masse
Le centre de masse (ou centre de gravité G) d'un objet, constitué de plusieurs petits objets, est situé aux coordonnées ( ![]() ) données (voir chapitre 5) par :
) données (voir chapitre 5) par :
![]()
où m est la masse de l'objet, mn et (xn , yn) la masse et la position du nième petit objet.
On pourrait aussi combiner le tout et dire que :
![]()
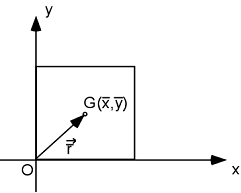
Bien sûr, si l'origine O du vecteur est située en G, alors ![]() =0.
=0.
Notes :
La vitesse du centre de masse est : ![]()
L'accélération du centre de masse est : ![]()
Travail fait par un couple lors d'une rotation
Travail fait par un couple lors d'une rotation
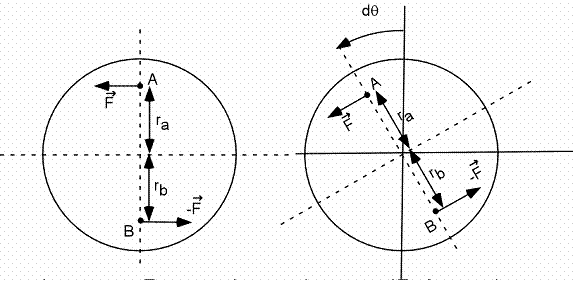
La grandeur du moment du couple est M= F(ra +rb)
Le travail fait = F(dsA )+F(dsB) = F (rad θ) +F (rB dθ ) = Mdθ
| Travail fait par un couple de moment M : |
|
Énergie cinétique de rotation
Un objet composé des particules 1,2,3.... est en rotation.
L'énergie cinétique est
K = ½m 1v 1 2 + ½m 2v 2 2+½m 3v 3 2+....
ou encore :
K = ½m 1(ωr1) 2+ ½m 2(ωr2) 2+ ½m 3(ωr3) 2 +....
ou encore :
K =½ω 2( m 1r 1 2 + m 2r 2 2+m 3r 3 2 +....)
ou encore :
| K = ½I ω 2 |
où I est le moment d'inertie de masse par rapport à l'axe de rotation.