Laboratoire 3: Énoncé

Objectifs: 

Ce laboratoire a pour but de vous :

• faire pratiquer l'écriture de sous-programmes;
• vous apprendre à subdiviser un programme en sous-programmes;
• de vous rappeler l'utilisation des structures de base: variables, boucles, structures conditionnelles..

Fonctionnement du laboratoire: 

• Ce laboratoire se compose de 10 exercices. Ceux-ci doivent tous être complétés d’ici la prochaine séance de laboratoire.
• Chaque exercice est accompagné d’indices. Il vous est conseillé de ne consulter l'indice qu'en cas de blocage.

Exercices

Pour tous les exercices, ci-dessous, lorsque l'exercice vous demande d'écrire une fonction vous devez également faire des appels à cette fonction depuis votre main. En règles générale (pas seulement pour le laboratoire), vous devez toujours tester vos fonction après les avoir implémentées en portant une attention particulière aux valeurs limites des paramètres. 

Exercice 1

Écrivez une fonction celcius_fahrenheit qui reçoit une valeur numérique exprimée en degrés Celcius et retourne la conversion de cette valeur en degrés Fahrenheit.

Exercice 2

La librairie "math.h" fournit une fonction log(double n) qui calcule le logarithme népérien de n. Cependant, nous aimerions calculer le logarithme dans n'importe quelle base. 

Écrire la fonction log_b qui prend deux valeurs: le nombre n dont on veut calculer le logarithme (réel), ainsi que la base b (entier). Votre fonction doit renvoyer le logarithme de n dans la base b.

Exercice 3

Écrire une fonction qui, à partir d'une date donnée (jour, mois et année) vous renvoie le jour de la semaine correspondant. Votre fonction devra renvoyer une valeur numérique correspondant au jour de la semaine: 0 pour dimanche, 1 pour lundi, ... 6 pour samedi. 

Pour ce faire, on utilisera l'algorithme de Mike Keith qui va comme suit: 

D = { [(23m)/9] + d + 4 + y + [z/4] - [z/100] + [z/400] - 2 } mod 7, si m>=3

D = { [(23m)/9] + d + 4 + y + [z/4] - [z/100] + [z/400] } mod 7, si m<3

Où : 

• d, m, y représentent respectivement le jour, le mois et l'année de la date; 
• z=y-1 si m<3, z=y si m>=3
• D est la valeur numérique du jour de la semaine résultant (de 0 à 6). 

Toutes les divisions sont des divisions entières.

Dans votre main, vous devez saisir la date et afficher à l'usager le jour correspondant (en toutes lettres)

Exercice 4

Écrire une fonction qui vous renvoie le nombre de chiffres d'un nombre. 

Exercice 5

Écrire une fonction qui vous renvoie le chiffre à une position donnée d'un nombre. Par exemple, la fonction appelée avec le nombre 15670 et la position 3, votre fonction doit renvoyer 6. 

Exercice 6

Écrire une fonction qui calcule la somme des chiffres d'un nombre. Votre fonction doit faire appel aux fonctions implémentées pour répondre aux questions 4 et 5.

Exercice 7

Écrire un programme qui affiche si un nombre est un palindrome. Un nombre est palindrome si ses derniers chiffres sont le miroir de ses premier chiffres. Par exemple, les nombres 123321 ou 3474743 sont des palindromes. 

Exercice 8

Écrire la fonction arc_tan qui reçoit une valeur x exprimée en radians (dans l'intervalle [-1, 1]) et retourne la valeur de l'arc tangente de x. Afin de trouver la valeur de l'arc tangente, utilisez la série ci-dessous, en faisant la somme jusqu'au 100ième terme. 

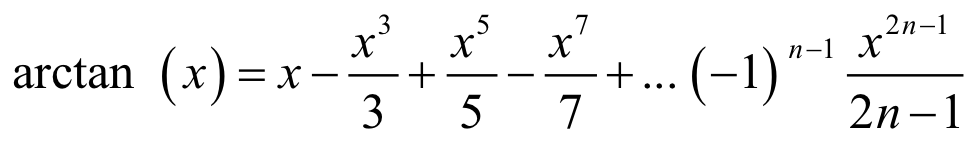
Exercice 9

Écrire une fonction pgcd qui calcule le plus grand commun diviseur de deux nombres. 

Exercice 10

Écrire une fonction qui affiche dans la console l'ensemble des nombres parfaits entre 0 et un nombre n fournit en paramètre. 

Un nombre est dit parfait si la somme de se diviseurs (autre que lui même) est égale au nombre lui même. Par exemple, 6 est nombre parfait car les diviseurs de 6 sont 1, 2 et 3 ; et 1+2+3 = 6. 

Pour traiter ce problème, vous devez subdiviser votre problème en sous-problèmes et resoudre chacun des sous-problèmes par une fonction.