La roue

Notes :

• Le cycliste n'est pas dessiné, mais il est là !
• On a omis la résistance de l'air (qui n'est pas négligeable, généralement), pour simplifier.

 

 

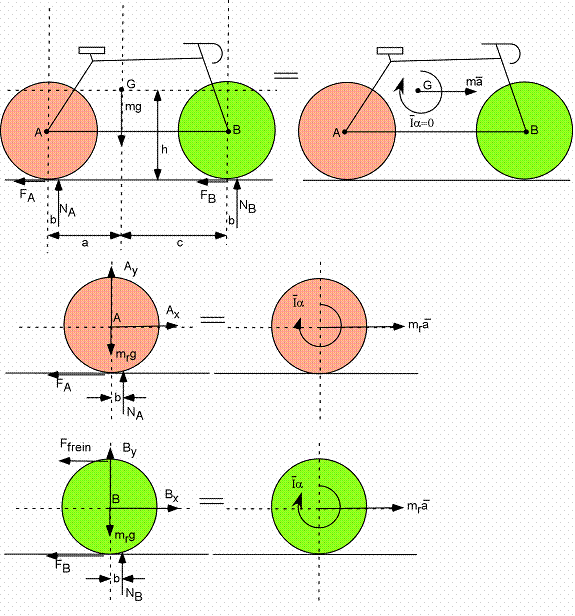
Bicyclette :

 

                    

 

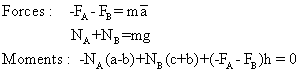
En combinant ces équations on trouve :

 

 

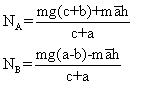
ici N_A > N_B ou N_B > N_A ..... tout dépend de . Si la décélération est trop grande ( très négative), alors N_A peut atteindre 0 et la bicyclette peut théoriquement basculer... En réalité, il y a souvent glissement plutôt que basculement.

Remarque : si le freinage est sur la roue arrière, il ne peut y avoir basculement (il ne peut y avoir, à l'arrière, à la fois freinage et perte de contact !).

 

Roue arrière :

 

 

Roue avant :

 

 

En additionnant les équations de moment sur les deux roues et comme et  :

 

 

et alors :

 

 

Si F_frein devient trop grand, F_B peut dépasser μ_s N_B et la roue peut glisser.

 

Énergie :

 

 

Travail de freinage (négatif)- énergie perdue par roulement = Variation (négative) de l'énergie cinétique de rotation (2 roues) et de l'énergie cinétique de translation.

Note : la résistance de l'air implique une perte d'énergie supplémentaire.