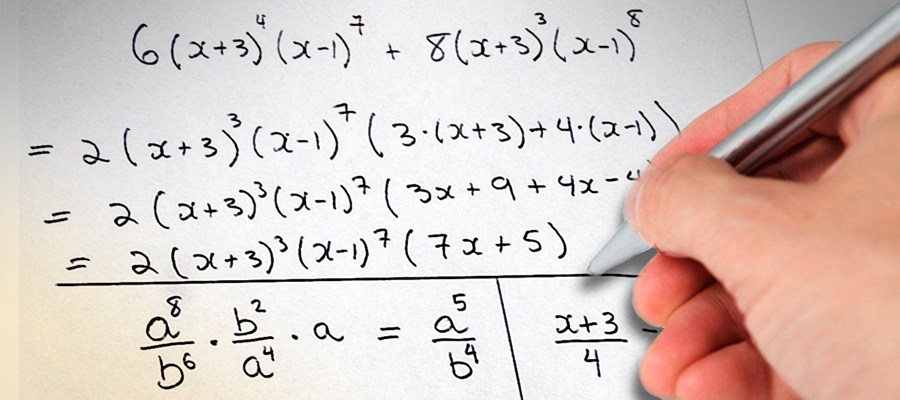MAT145 Calcul différentiel et intégral
Résumé de section
Maîtriser des notions de calcul différentiel et intégral utilisées dans les autres cours de mathématiques et dans les cours de génie.
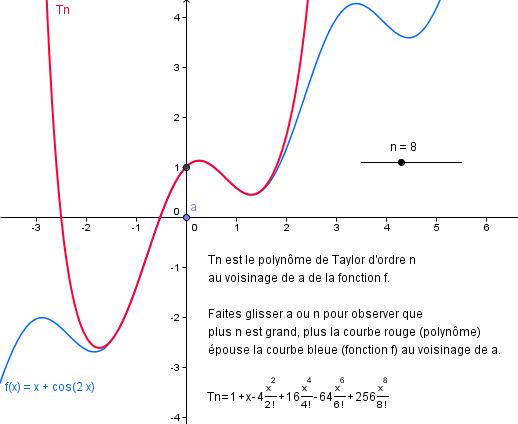
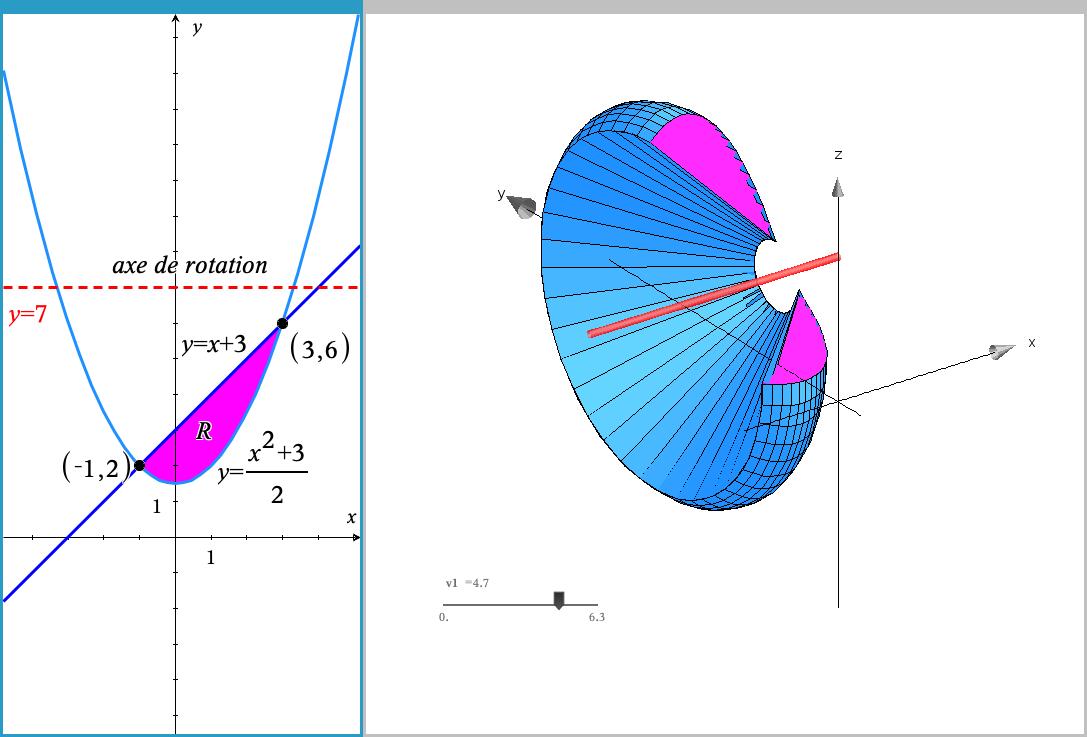
Analyse : généralités sur les fonctions de R dans R; calcul différentiel : limites, dérivée, dérivée des fonctions élémentaires, règles de dérivation, étude de graphe, optimisation, etc. Calcul intégral : intégrales indéfinies, méthode d'intégration, utilisation des tables, intégrales définies, application (calcul d'aires, de volumes, de longueurs d'arc), méthodes numériques, intégrales impropres, etc. Suites et séries. Développements limités (Taylor, MacLaurin), évaluation de fonctions et d'intégrales définies à l'aide des séries.
Une liste complète des groupes, des enseignants et leurs coordonnées, ainsi que le responsable du cours se trouve dans le plan de cours, sous l'onglet Accueil.
-
 Hughes-Hallett, Doborah, et Andrew M. Gleason. 1999. Fonctions d'une variable : calcul différentiel et intégral : le projet Harvard. Montréal: Chenelière/McGraw-Hill, 596 p.
Hughes-Hallett, Doborah, et Andrew M. Gleason. 1999. Fonctions d'une variable : calcul différentiel et intégral : le projet Harvard. Montréal: Chenelière/McGraw-Hill, 596 p. -
 Stewart, James. 2011. Analyse : concepts et contextes : volume 1 : fonctions d'une variable, 3e éd. Bruxelles: De Boeck.
Stewart, James. 2011. Analyse : concepts et contextes : volume 1 : fonctions d'une variable, 3e éd. Bruxelles: De Boeck.
-
Vidéo interactive sur quatre questions d'algèbre.

 MAT145 Calcul différentiel et intégral
MAT145 Calcul différentiel et intégral